Summary
当前深度神经网络方法存在问题:Large deep neural networks are powerful, but exhibit undesirable behaviors such as memorization and sensitivity to adversarial examples
论文核心思想:Mixup trains a neural network on convex combinations of pairs of examples and their labels
取得结果:mixup improves the generalization of state-of-the-art neural network architectures, reduces the memorization of corrupt labels, increases the robustness to adversarial examples, and stabilizes the training of generative adversarial networks
Introduction
论文首先引入了两个概念:Empirical Risk Minimization (ERM) Principle and Vicinal Risk Minimization (VRM) Principle, 即经验风险最小化原则和邻近风险最小化原则。
经验风险最小化是当前机器学习训练方法的基本原则,即对模型进行训练并期在此过程将训练数据的平均误差最小化,同时经典对学习理论已经揭示,只要学习模型(如神经网络)的规模不随训练数据的数量增加而增加,ERM 的收敛性就可以得到保证。这里的模型规模可以使用模型参数或者其VC复杂度来衡量。
然而,这与当前的研究范式有所冲突,当前的模型不断的增加训练数据集和模型参数,以追求更好的效果,这些模型很大程度上都是在对训练数据进行记忆而非泛化概括。另一方面,基于 ERM 原则训练的模型,对于 OOD 的样本(不在训练样本分布内)或者对抗性样本的表现非常不稳定。
在与训练数据相似但不同的数据上进行训练的方法被称作数据增强训练,其是邻近风险最小化原则的形式化表现。VRM 通常需要专业知识描述训练数据中每个样本的邻域,从而可以从训练样本邻域中提取附加的虚拟样本以扩充对训练分布的支持,这一操作扩大了训练样本分布范围或者可以说是对训练数据的更精准详细的概率分布的模拟。数据增强可以提高泛化能力,但这一过程往往依赖于训练数据集,而且需要专门知识。其次,数据增强假定领域内样本都是同一类,且没有对不同类不同样本之间领域关系进行建模。
论文提出了一种简单的数据未知的数据增强方法——mixup,通过结合先验知识,即特征向量的线性插值应导致相关标签的线性插值,来扩展训练分布。其构建扩充样本的一种方式如下:
其中$x_i, x_j$原始输入向量,$y_i, y_j$是one-hot向量,$(x_i, y_i), (x_j, y_j)$是训练数据,$\lambda \in [0,1]$,这种方式对输入特征和目标均进行线性加权操作。其训练过程中对损失计算处理不需要进行额外的修改:
mixup 的实现还有另一种方式,对 feature 进行插值得到新样本,但对targets不进行插值计算,而是通过修改 loss 来实现:
此时不需要$y_i, y_j$是one-hot向量。
mixup 的数据增强方法以 batch 为单位进行操作,可以是同一个batch数据内部, 也可以在不同 batch 数据之间。
这两种方式是等价的,只是对于目标输出的处理不同导致使用不同的loss计算方式。
Experiments
预实验

上左图为 mixup 的一种简单代码实现,右图为 mixup 的对分类标签分布对影响,使得标签与标签之间分布转换更具有线性的连续性过渡。
beta分布对超参数 $\alpha$的作用:
The mixup hyper-parameter $\alpha$ controls the strength of interpolation between feature-target pairs, recovering the ERM principle as $\alpha \to 0$.
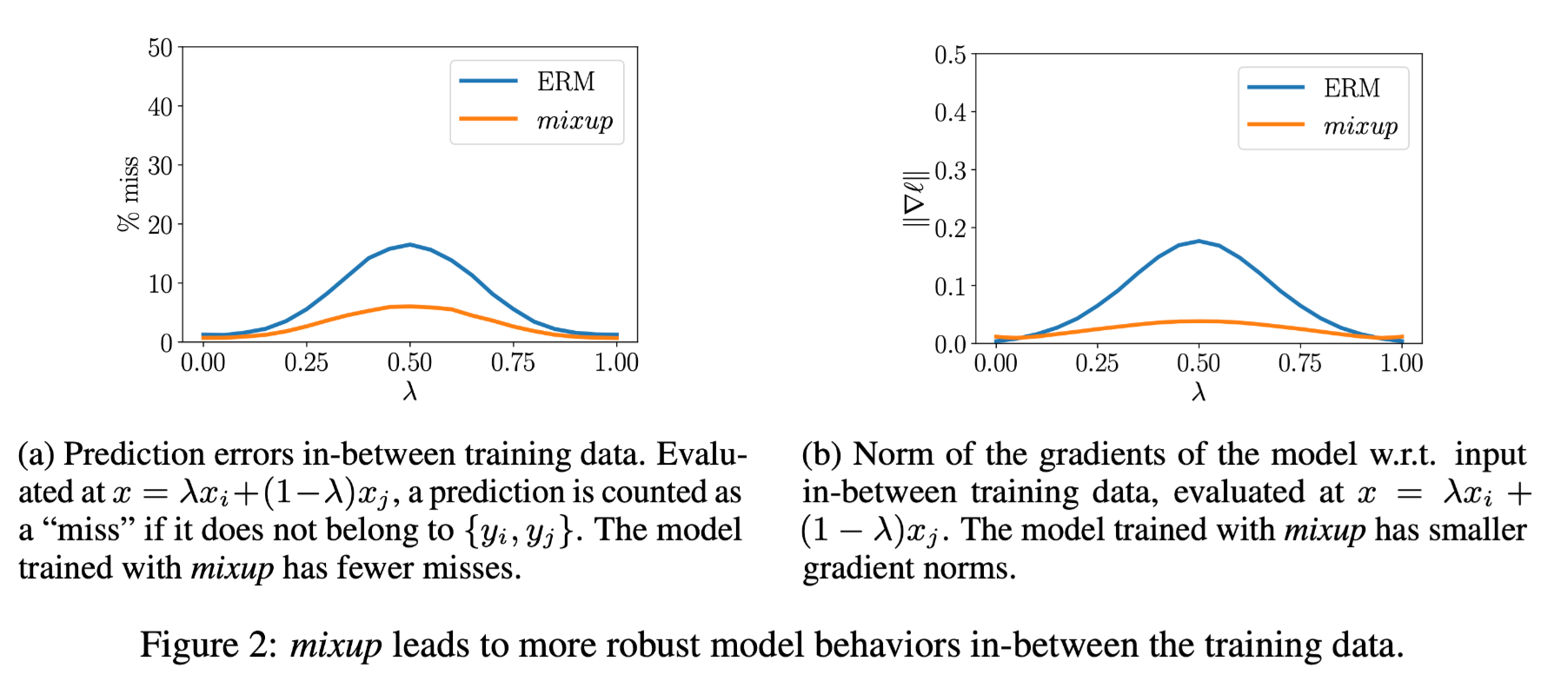
The mixup vicinal distribution can be understood as a form of data augmentation that encourages the model $f$ to behave linearly in-between training examples. We argue that this linear behaviour reduces the amount of undesirable oscillations when predicting outside the training examples.
即 mixup 的线性插值增强使得模型对于训练样本的表现也更具有线性的连续性,减少模型在训练样本分布外的预测偏差。同时在训练样本分布内的预测误差更小,
图像分类表现
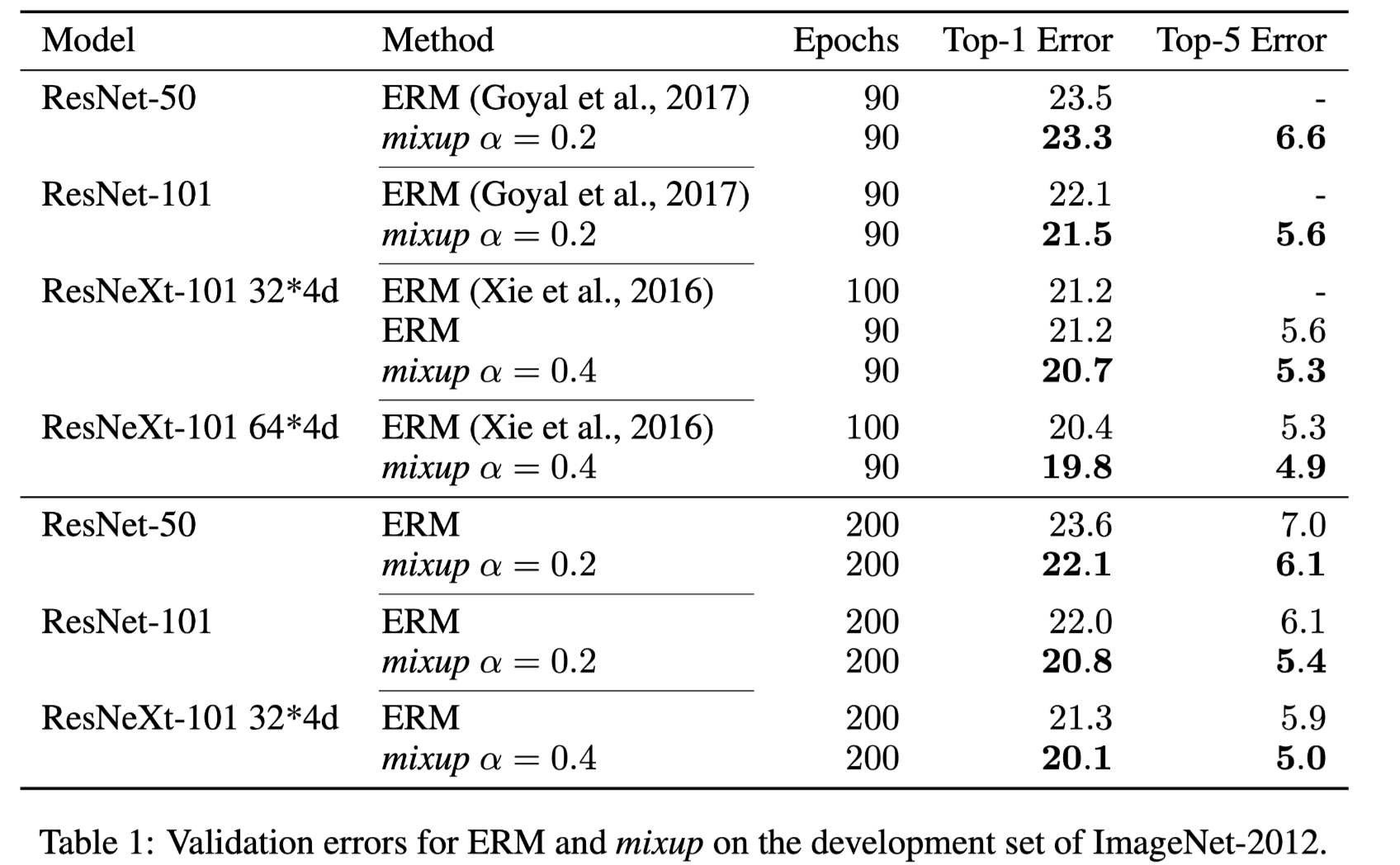
ImageNet-2012的分类实验发现:
we find that α ∈ [0.1, 0.4] leads to improved performance over ERM, whereas for large α, mixup leads to underfitting. We also find that models with higher capacities and/or longer training runs are the ones to benefit the most from mixup.

上图为在 CIFAR-10 and CIFAR-100 classification problems 的对比实验表现。
SPEECH DATA 实验表现

上图为 Classification errors of ERM and mixup on the Google commands dataset.
具体处理:
For speech data, it is reasonable to apply mixup both at the waveform and spectrogram levels. Here, we apply mixup at the spectrogram level just before feeding the data to the network.
MEMORIZATION OF CORRUPTED LABELS 实验
对数据集进行预处理:
Generate three CIFAR-10 training sets, where 20%, 50%, or 80% of the labels are replaced by random noise, respectively. All the test labels are kept intact for evaluation
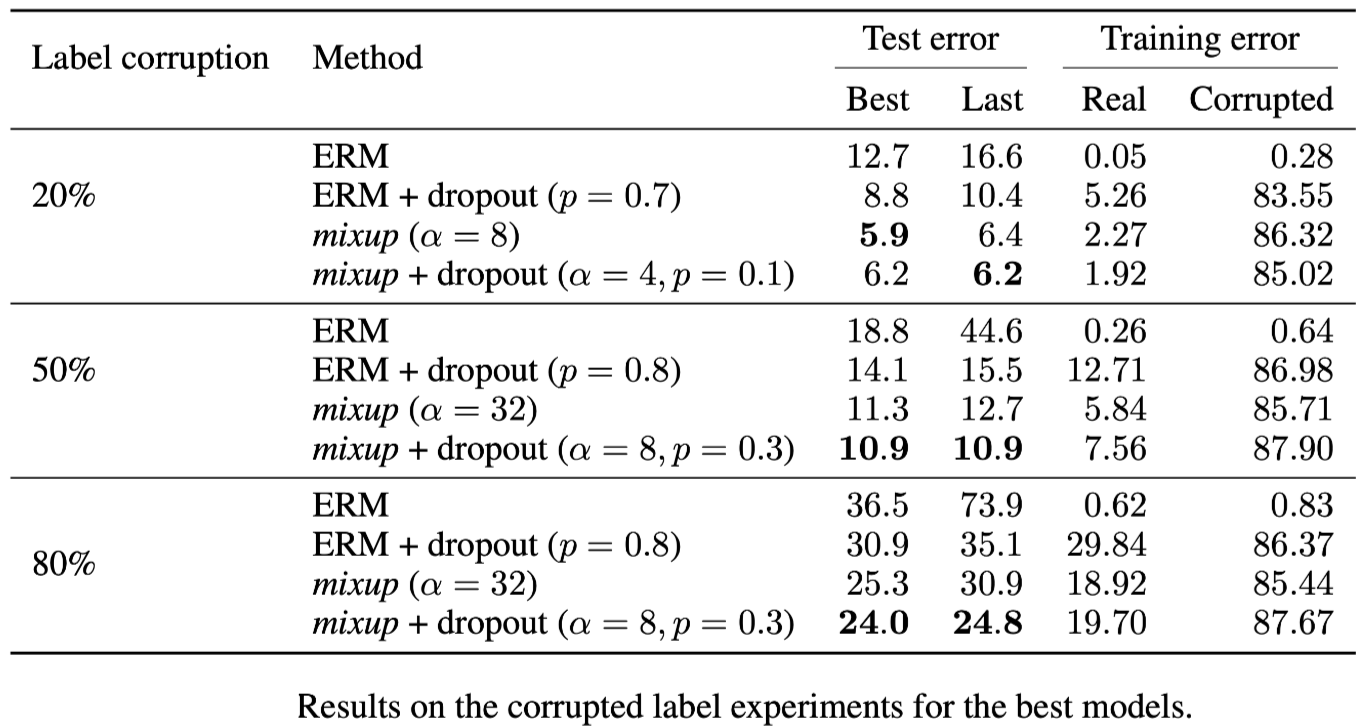
To quantify the amount of memorization, we also evaluate the training errors at the last epoch on real labels and corrupted labels
实验发现:
To quantify the amount of memorization, we also evaluate the training errors at the last epoch on real labels and corrupted labels
ROBUSTNESS TO ADVERSARIAL EXAMPLES 实验
mixup 对于模型鲁棒性的影响实验,其中对抗性样本的产生:
Adversarial examples are obtained by adding tiny (visually imperceptible) perturbations to legitimate examples in order to deteriorate the performance of the model. The adversarial noise is generated by ascending the gradient of the loss surface with respect to the legitimate example.
实验结果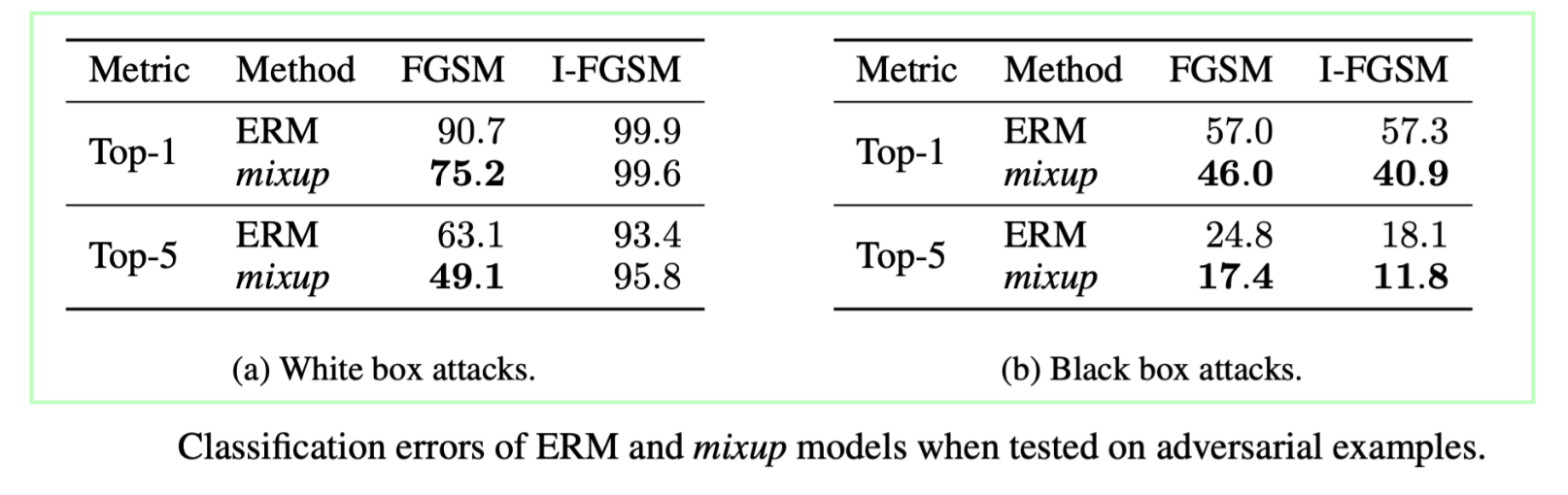
其中白盒攻击实验:
for each of the two models, we use the model itself to generate adversarial examples, either using the Fast Gradient Sign Method (FGSM) or the Iterative FGSM (I-FGSM) methods (Goodfellow et al., 2015), allowing a maximum perturbation of $\epsilon = 4$ for every pixel. For I-FGSM, we use 10 iterations with equal step size
黑盒攻击实验:
we use the first ERM model to produce adversarial examples using FGSM and I-FGSM. Then, we test the robustness of the second ERM model and the mixup model to these examples
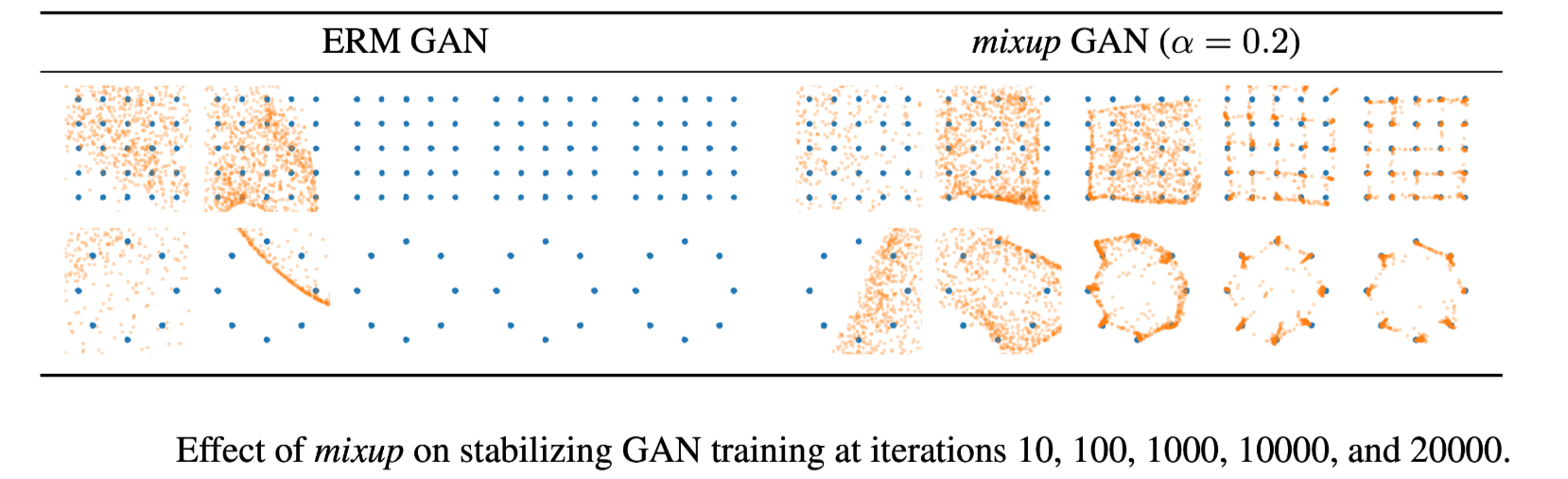
STABILIZATION OF GANs 实验
We argue that mixup should stabilize GAN training because it acts as a regularizer on the gradients of the discriminator.
Then, the smoothness of the discriminator guarantees a stable source of gradient information to the generator.
加入了 mixup 的形式化后的 GAN 为:
ABLATION STUDIES 实验
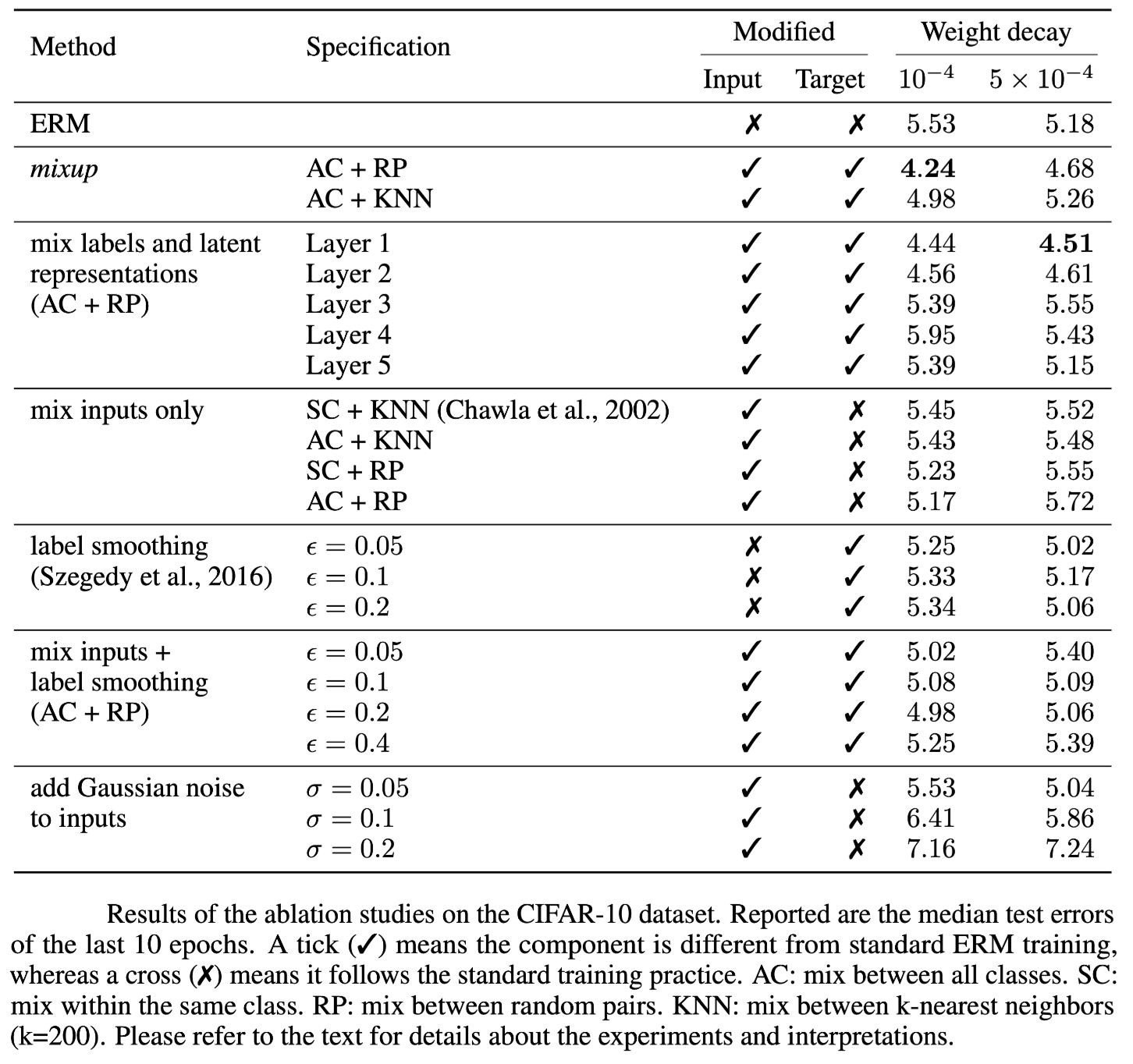
mixup 是直接进行样本(输入和输出)插值的数据增强方法,但是在增强输入的时候,可以选择对神经网络的潜在表示(即feature maps)进行插值,也可以选择只在最近邻之间进行插值,或者只在同一类的输入之间进行插值。当要插值的输入来自两个不同的类时,我们可以选择为合成输入指定一个标签,例如使用在凸组合中权重更大的输入标签。消融实验主要在这些可能性的选择中进行。
消融实验发现:
mixup 最优,且明显优于次优方案 mix input + label smoothing
正则化的影响如上表所示,REM 较大的权重衰减合适,mixup相反,表明mixup本身可以为模型带来一定的正则化影响,提高模型的泛化性和鲁棒性
在高层次特征表示进行插值时使用大的权重衰减有益处,表明增加了正则化影响
插值方法的对比:Among all the input interpolation methods, mixing random pairs from all classes (AC + RP) has the strongest regularization effect.Label smoothing and adding Gaussian noise have a relatively small regularization effect.
SMOTE方法的影响:Finally, we note that the SMOTE algorithm does not lead to a noticeable gain in performance.
Conclusion
With increasingly large $α$, the training error on real data increases, while the generalization gap decreases. This sustains our hypothesis that mixup implicitly controls model complexity. However, we do not yet have a good theory for understanding the ‘sweet spot’ of this bias-variance trade-off.
随着参数$\alpha$的增大,实际数据的训练误差增大,而泛化差距减小。这支持了我们的假设,即mixup方法隐式控制着模型的复杂性。然而,我们还没有一个好的理论来理解这种偏差-方差权衡的“最佳点”。
同时,是否可以把这个思想应用到回归预测和结构性预测中?
这种方法是否不仅仅在监督学习中有效?
这种方法能否进一步保证模型处理 OOD 数据的鲁棒性?
阅读总结
这篇论文提出了一个朴素简单的数据增强方法,直接对训练样本进行插值混合,对应的标签也进行插值混合,当然这种方法比较适用于像图像这种连续数值的数据,对于文本数据不能直接照搬。如何为文本数据增强提供参考和可能性是一个值得思考的问题。
这篇文章的另一个值得学习的地方在于进行了一系列的充分的实验分析,从达到图像分类的新SOTA,到证明能够提高模型的在面对对抗性样本和错误标签样本的鲁棒性,最终还实验分析了mixup可以泛化到语音数据和表格化数据,可以用来稳定GANs的训练。
同时为了进一步明确mixup的各个操作的选择性,作者进行了一系列的消融实验,并得到了相关结论和发现。

