背景
本章主要为了后续章节做背景知识的铺垫。主要回顾了之后提出的理论相关的概率论和信息论的基础。
对与机器学习也特定的回顾了将要用的部分,最后对 NLP 的主要任务进行了概览。
概率论与信息论
概率论为我们提供了讨论和分析这篇论文中提出的许多本质上是概率性的方法的通用语。
通过概率论,我们可以在已经发生了其他事件的情况下,对某个事件发生的可能性做出判断。并对可能计算。
信息论同样为我们提供了描述事件中编码的信息的工具和描述信息差异的方法。后者是一个我们使用机器学习方法时经常想要最小化的属性。
概率论基础
随机变量:概率论理论的核心是随机变量,即是按照一定的随机分布产生的变量值。在本论文中我们的目标的就是构建一个能够对这些随机变量的随机分布建模的系统。
PMF(probability mass function):如果$X$离散型随机变量,定义概率质量函数为$f_X(x)$, PMF 其实就是高中所学的离散型随机变量的分布律。即是
PDF(probability density function):如果$X$是连续型随机变量,定义概率密度函数为$f_X(x)$,用 PDF 在某一区间上的积分来刻画随机变量落在这个区间中的概率,即:
如果二维随机变量$(x,y)$全部可能取到的值是有限对或可列无限多对,则称$(x,y)$是离散型的随机变量。
设二维离散型随机变量$(x,y)$所有可能取得值为$(x_i,y_j), i,j=1,2,3,\cdots$,记$P(X=x_i, Y=y_j) = p_{i,j}, i,j=1,2,\cdots$,并满足
- 联合概率分布(joint probability distribution):包含多个条件且所有条件同时成立的概率,即是$P(X=x_i, Y=y_j) = p_{i,j}, i,j=1,2,\cdots$为二维离散型随机变量(X,Y)的分布律,或称随机变量X和Y的联合分布律。
- 计算方法:$P(X=x_i, Y=y_j) = P(Y=j\mid X=i)P(X=i) , i,j=1,2,\cdots$
- 边缘概率分布(marginal probability distribution):对于离散型随机变量,可得 X 和 Y的边缘分布函数:$P_{i\cdot} = \sum^\infty_{j=1}p_{i,j} = P\{X=x_i\},i=1,2,\cdots$以及$P_{j\cdot} = \sum^\infty_{i=1}p_{i,j} = P\{Y=y_i\},i=1,2,\cdots$
- 条件概率分布(conditional probability distribution):设 A 与 B 为样本空间 Ω 中的两个事件,其中 P(B)>0。那么在事件 B 发生的条件下,事件 A 发生的条件概率为$P(A\mid B)= \frac{P(A\cap B)}{P(B)}$,条件概率有时候也称为:后验概率。
贝叶斯规则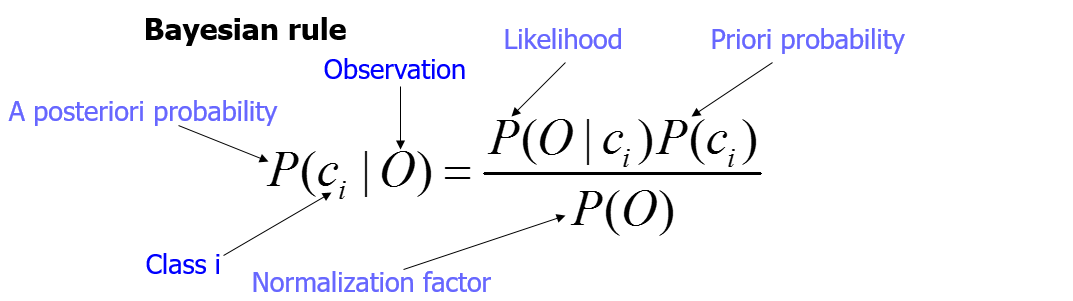
其他一些概念:期望、方差、独立性假设等等。
常见的分布:
- 伯努利分布
- 高斯分布
- 经验分布
信息论
在这篇论文中,我们将使用信息论的方法来描述两个概率分布在信息编码方面的差异。这将为我们提供一种度量,即我们的模型正在学习的概率分布与数据的经验分布相比是否“良好”。
信息论入门介绍的文章参见这里

